The Reports page allows you to run Cost Monte Carlo reports of the tasks in the project, such as: Cumulative Curves, Tornado and Status. The reports are run based on the scenario applied for the project.
Monte Carlo Charts:

Figure 1
Cumulative Curves:
The Cumulative Curves report includes Cumulative S Curve with Risk Events, Cumulative S Curve without Risk Events and Delta of Cumulatives. The Cumulative Curve report shows the distribution of the estimated cost exposure of a selected project or task. It simulates cost values based on distribution types. The columns show the hits for each of the total amount of task simulation cost exposure.
The steps that are carried out to generate Cumulative Curves chart are follows:
Step 1: Generate risk groups for the given correlations. Grouping is done such that all the tasks that are correlated with one another are considered as a group.
Step 2: Generate correlated random values for each risk group. The static calculation is explained below:
a) Create a correlation matrix with correlation coefficients such that task which is more correlated comes in the first row.
A correlation matrix is used to investigate the dependence between multiple variables at the same time. The result is a table containing the correlation coefficients between each variable and the others.
b) Calculate unspecified coefficients in the matrix from correlation of two related specified correlation coefficients.
b.1: Find Eigen values and Eigen vectors matrices of the inconsistent correlation matrix.
b.2: Replace the non-positive Eigen values with the smallest positive double number.
b.3: Create a Diagonal Matrix of Sqrt (1 / (Eigen Vectors^2 * Eigen Values))
b.4: Create a Diagonal Matrix of Sqrt (Eigen Values)
b.5: Multiply the diagonal matrix in step 3 with Eigen vectors matrix which is multiplied the matrix in step 4.
i.e., Diagonal Matrix of Sqrt (1 / (Eigen Vector^2 * Eigen Values)) * Eigen Vector * Diagonal Matrix of Sqrt (Eigen Values)
b.6: Multiply the matrix got from step 5 with its transpose. Now we will get the correlation matrix which is consistent.
b.7: Replacing the inconsistent coefficients with coefficients calculated from consistent coefficients.
? = (6 * asin(Correlation Coefficient / 2) / ?) * 100
c) Perform Cholesky decomposition of the correlation matrix (CHOL). If exception occurs, then the correlation matrix is inconsistent. Then the simulation is stopped and asks the user whether to adjust correlations of the risk group automatically or not. If no exception occurs, then perform the remaining steps.
The Cholesky decomposition or Cholesky factorization is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose, which is useful example for efficient numerical solutions and Monte Carlo simulations.
d) Create a matrix (R) with number of rows is equal to iteration times and number of columns equal to number of tasks in the risk group with randomly generated values which are normally distributed with mean 0 and SD 1.
e) Multiply the matrix generated in (d) with matrix generated by Cholesky decomposition. This gives the normally distributed random values with correlation (these values used in normally distributed durations). To get it uniformly distributed, find the cumulative distribution function of the matrix (these values are used for other distributions). Each columns will have the random values for corresponding task durations.
i.e., correlated random value matrix CRM is
CRM = R * CHOL, if normal distribution
CRM = pnorm(R * CHOL), if not normal distribution
The cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Example
An example for normal distribution with 10 iterations is given below.
a) Let A, B, C, D are correlated such that corr (A, B) = 60%, corr (A, C) = 70%, corr (A, D) = 80%. Now we have one risk group ABCD.
b) Correlation Matrix with user specified correlation coefficients
| 1.0 | 0.6 | 0.7 | 0.8 |
| 0.6 | 1.0 | 0.0 | 0.0 |
| 0.7 | 0.0 | 1.0 | 0.0 |
| 0.8 | 0.0 | 0.0 | 1.0 |
Table 1
c) Correlation Matrix after calculating all correlation coefficients
| 1.0 | 0.5112 | 0.5936 | 0.6748 |
| 0.5112 | 1.0 | 0.0302 | 0.0343 |
| 0.5936 | 0.0302 | 1.0 | 0.0398 |
| 0.6748 | 0.0343 | 0.0398 | 1.0 |
Table 2
d) Matrix with random values, R
| -0.22759883330513203 | -0.14779528819416274 | -0.8116534929634235 | -1.3828258408574279 |
| -0.6257058657442784 | 0.22979287727014666 | 0.6940068141614696 | -1.2819970948797965 |
| 0.9606080643281025 | 0.12951392609894774 | 0.9969510606030434 | 0.5490356353852022 |
| -1.0168529345485386 | -0.7515175581895532 | 0.33692856764956125 | -1.3325301102147291 |
| -0.672674228450859 | 0.8940508933639131 | -1.5357821937125395 | -0.38541097828943366 |
| 0.8837124607600431 | 0.21956223049086745 | 0.4804300141584299 | 0.8033496303121265 |
| -2.080382126627115 | -1.4204197286554967 | -0.8921771773333548 | -1.4384490197892787 |
| -0.9457988314984864 | -0.16309395713329183 | -0.30523272399453705 | -1.0969624106348446 |
| -0.6255515357453936 | 1.2239957073107248 | -0.36742658070420897 | -1.5732911013915596 |
| -0.0612578037946805 | -0.34877000727229757 | -1.1554191662901698 | 1.1669823548362461 |
Table 3
e) Matrix with correlated random values
| Task A | Task B | Task C | Task D |
| -0.22759883330513203 | -0.14779528819416274 | -0.8116534929634235 | -1.3828258408574279 |
| -0.6257058657442784 | 0.22979287727014666 | 0.6940068141614696 | -1.2819970948797965 |
| 0.9606080643281025 | 0.12951392609894774 | 0.9969510606030434 | 0.5490356353852022 |
| -1.0168529345485386 | -0.7515175581895532 | 0.33692856764956125 | -1.3325301102147291 |
| -0.672674228450859 | 0.8940508933639131 | -1.5357821937125395 | -0.38541097828943366 |
| 0.8837124607600431 | 0.21956223049086745 | 0.4804300141584299 | 0.8033496303121265 |
| -2.080382126627115 | -1.4204197286554967 | -0.8921771773333548 | -1.4384490197892787 |
| -0.9457988314984864 | -0.16309395713329183 | -0.30523272399453705 | -1.0969624106348446 |
| -0.6255515357453936 | 1.2239957073107248 | -0.36742658070420897 | -1.5732911013915596 |
| -0.0612578037946805 | -0.34877000727229757 | -1.1554191662901698 | 1.1669823548362461 |
Table 4
Each column in the matrix contains the random values for corresponding tasks for each iteration.
Step 3: Generate random values for resources of those tasks which are not correlated.
Step 4: Generate random values for resource rates of those tasks which are not correlated.
Step 5: Set the random values of resources as random values for resource rates of those tasks which are correlated.
Step 6: For each resource of a task generate values based on the distribution and number of iterations with given uncertainties. For import type “Multiple Resources”, there can be multiple resources for a task and the uncertainties may be different for each of them.
Step 7: Generate values based on the distribution and number of iterations with given uncertainties for corresponding resource rate of each resource. For import type “Simple Uncertainty”, the values will be same for all iteration.
Step 8: For each iteration, multiply the values of resource and resource rate respectively to find the cost for each resource.
Step 9: For each iteration, add the cost of all resources.
Cumulative S Curve with Risk Events:
The Cumulative S Curve report shows the distribution of the estimated cost exposure of a selected project or task. It simulates cost values based on distribution types. The columns show the hits for each of the total amount of task simulation cost exposure. The S curve shows the cumulative frequency of the hits in percentage. To get individual task´s Cumulative S Curve report, select the task from the PROJECT REPORT dropdown.
Steps:
- Cost Analysis—>Reports
- Click Cumulative S Curve with Risk Events link under Cumulative Curves. (Figure 1)
- Select the Bar width and set the Iteration Times and then click RUN ANALYSIS. (Figure 2) The chart generated and the table is shown in the Figure 2

Figure 2
Cumulative S Curve without Risk Events:
The Cumulative S Curve report shows the distribution of the estimated cost exposure of a selected project or task without considering the risks associated with it. It simulates cost values based on distribution types. The columns show the hits for each of the total amount of task simulation cost exposure. The S curve shows the cumulative frequency of the hits in percentage.
Steps:
- Cost Analysis—>Reports
- Click Cumulative S Curve without Risks link under Cumulative Curves. (Figure 1)
- Select the Bar width and set the Iteration Times and then click RUN ANALYSIS. (Figure 3) The chart generated and the table is shown in the Figure 3.

Figure 3
Delta of Cumulatives:
The Delta of Cumulative chart shows the variation S Curve of costs with risk and without risk.
Steps:
- Cost Analysis—>Reports
- Click Delta of Cumulatives link under Cumulative Curves. (Figure 1)
- Set the Iteration Times and then click RUN ANALYSIS. (Figure 4) The chart generated and the table is shown in the Figure 4

Figure 4
Tornado Charts:
The Cost Values with Risk Events Isolated To P, Cost Percentages with Risk Events Isolated To P, Cost Values without Risk Events Isolated To P, Cost Percentages without Risk Events Isolated To P and Correlation Isolated to P reports are Tornado Charts that depends on the simulated cost exposure values of each task up to the Pn iteration value, where `n´ is the percentile value of total number of iterations given. The x axis represents the cost exposure and the y axis represents the task names.
Cost Values with Risk Events Isolated To P:

Figure 5
Cost Percentages with Risk Events Isolated To P:

Figure 6
Cost Values without Risk Events Isolated To P:

Figure 7
Cost Percentages without Risk Events Isolated To P:

Figure 8
Correlation Isolated to P:
The step to generate the Correlation Isolated to P (n) chart is:
Pearson correlation coefficient for Total cost up to p(n) and Task cost up to p(n) * 100

Figure 9
Status charts:
This Monte Carlo chart is a pie chart which shows the total number of tasks included in the project. And the number of risks mapped to the tasks as threat and opportunities are also counted.
Steps:
- Cost Analysis —> Reports
- Click Status link under Monte Carlo Charts. (Figure 3) The chart generated and the table is shown in the Figure 10

Figure 10
Delta Of Cumulative (Comprehensive):
Steps:
- Cost Analysis—>Reports
- Click Delta of Cumulatives (Comprehensive) link under Cumulative Curves. (Figure 1)
- Set the Iteration Times and Select Highlighters then click RUN ANALYSIS (Figure 11) The chart generated and the table is shown in the Figure 11

Figure 11
Delta Of Cumulative (Normalized):
Steps:
- Cost Analysis—>Reports
- Click Delta of Cumulatives (Normalized) link under Cumulative Curves. (Figure 1)
- Set the Iteration Times and Select Highlighters then click RUN ANALYSIS (Figure 12) The chart generated and the table is shown in the Figure 12

Figure 12
Tornado charts:
Iteration Data Set:
This functionality is used to export the tasks with risk events and without risk events along with Task Id, Task Name and Budgeted Cost of the selected project to MS Excel. A sample spreadsheet is shown in Figure 13. Iterations value are calculated for each task separately based on the number of iteration specified.
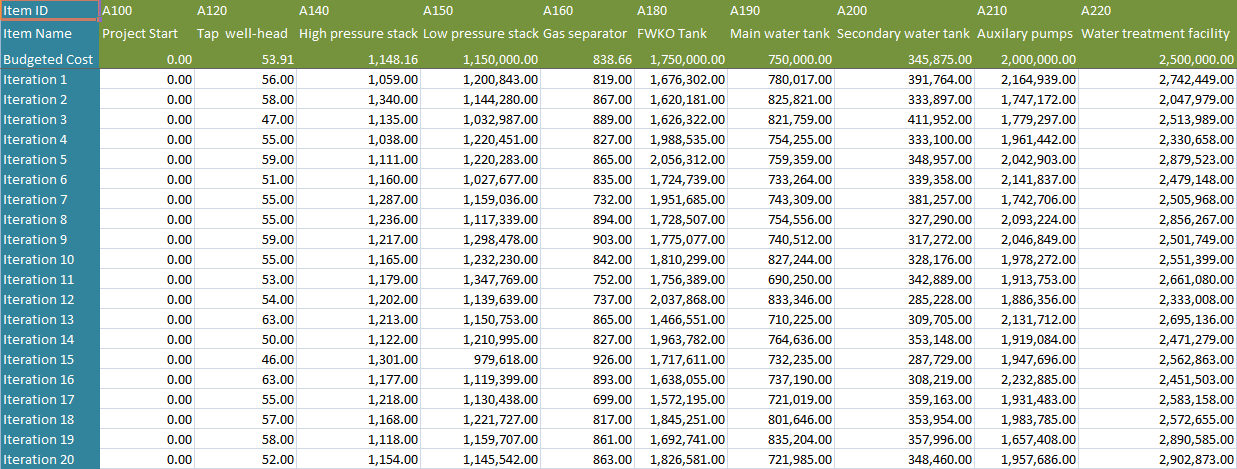
Figure 13
Correlation Matrix:
This functionality is used to generate a matrix of correlations existing between the tasks in the selected project. A sample spreadsheet is shown in Figure 14.
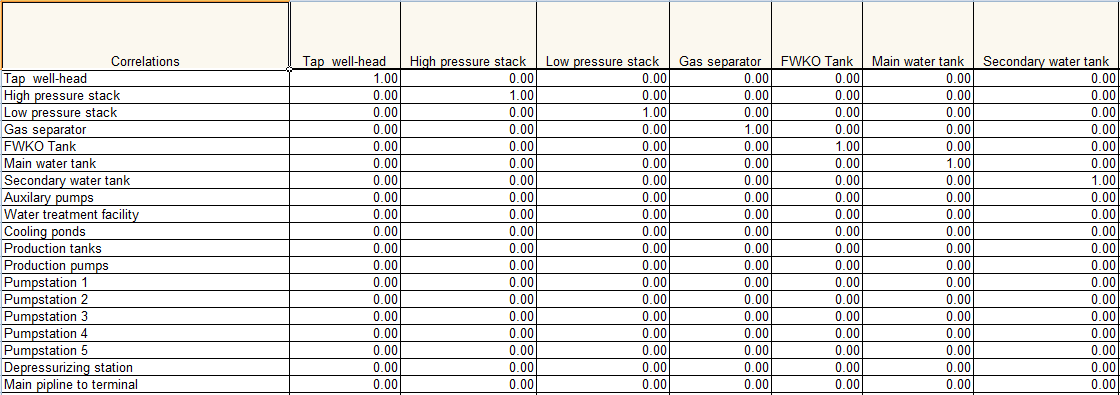
Figure 14
Correlation:
This functionality is used to generate the correlation between the tasks and their details in a tabular format. The columns to be displayed are determined by the selected column order in correlation page in the application. A sample spreadsheet is shown in Figure 15.
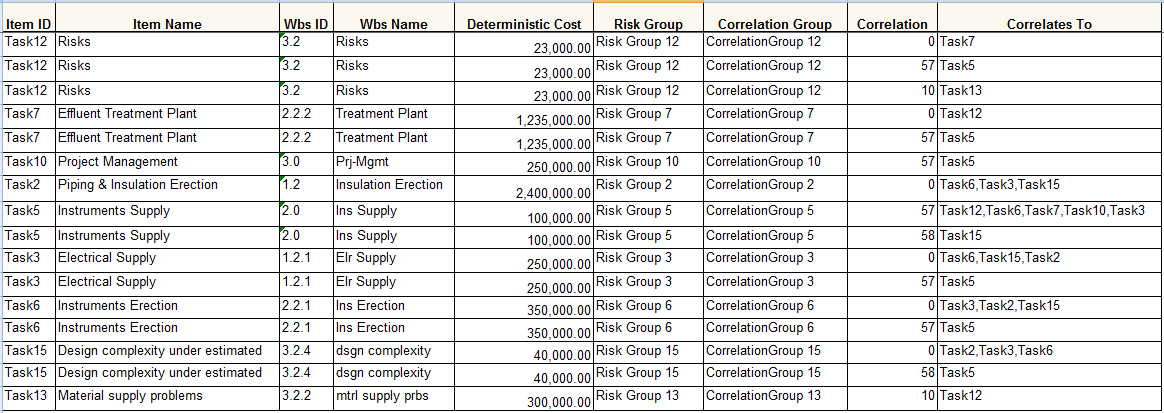
Figure 15
Export to Word:
This functionality is used to export the Cost Monte Carlo reports and data table as a Word document.
Steps:
- Cost Analysis —> Reports
- Click the Export to Word link. (Figure 2)
Export to PowerPoint:
This functionality is used to export the Cost Monte Carlo reports generated to Power Point.
Steps:
- Cost Analysis —> Reports
- Click the Export to PowerPoint link. (Figure 2)
Export to Excel:
This functionality is used to export the Cost Monte Carlo reports as an excel file.
Steps:
- Cost Analysis —> Reports
- Click the Export to Excel link. (Figure 2)
Export to Excel (Plot Points) for Cumulative Curve Reports
This functionality is used to export the Cost Monte Carlo reports as an excel file which gives details of number of hits for particular range of cost (cumulative frequency).
Steps:
- Cost Analysis —> Reports
- Click the Export to Excel (Plot Points) link. (Figure 4)